Exercices
Exercice 1 : Sélection des échelles spatiales et temporelles
Choisissez l'échelle spatiale et temporelle appropriée pour décrire le mouvement du système dans chacune des situations suivantes
- Une balle lancée par un joueur de basket pour un tir à trois points.
- Un avion de ligne en vol transatlantique de Paris à New York.
- Une plaque tectonique se déplaçant de quelques centimètres par an.
- Une fourmi parcourant une distance de quelques mètres dans un jardin.
- La rotation d'une aiguille de montre.
- Un athlète courant le marathon.
- Les mouvements des aiguilles sur un cadran solaire.
- La croissance d'un arbre au fil des saisons.
- Une étoile filante traversant le ciel nocturne.
- Les mouvements d'une bactérie observés au microscope.
- Échelle spatiale : mètres ; Échelle temporelle : secondes. La balle parcourt une courte distance en un temps bref, idéal pour l'analyse du tir.
- Échelle spatiale : kilomètres ; Échelle temporelle : heures. L'avion couvre de grandes distances sur une période prolongée, approprié pour les vols long-courriers.
- Échelle spatiale : kilomètres ; Échelle temporelle : années. Le mouvement des plaques est très lent et sur de grandes échelles géographiques.
- Échelle spatiale : mètres ; Échelle temporelle : minutes. Une fourmi se déplace rapidement sur une petite échelle.
- Échelle spatiale : millimètres ; Échelle temporelle : secondes. La précision et la rapidité sont nécessaires pour observer la rotation de l'aiguille.
- Échelle spatiale : kilomètres ; Échelle temporelle : heures. La distance parcourue pendant un marathon et le temps pris sont significatifs à cette échelle.
- Échelle spatiale : centimètres ; Échelle temporelle : heures. Les mouvements lents du cadran solaire sont mieux observés sur une longue période.
- Échelle spatiale : mètres ; Échelle temporelle : années. La croissance d'un arbre est un processus lent qui se mesure en années.
- Échelle spatiale : kilomètres ; Échelle temporelle : secondes. Les étoiles filantes traversent rapidement le ciel et couvrent de longues distances.
- Échelle spatiale : micromètres ; Échelle temporelle : secondes. Les bactéries sont petites et leurs mouvements rapides nécessitent une observation minutieuse.
Exercice 2 : Choix du référentiel
Pour chacune des situations suivantes, choisissez le référentiel le plus approprié pour décrire le mouvement du système et justifiez votre choix.
- Un passager marchant dans un train qui démarre. Devriez-vous choisir un référentiel lié au train ou à la gare pour décrire le mouvement du passager ? Justifiez votre choix.
- Un satellite en orbite autour de la Terre. Quel serait le référentiel le plus approprié : un référentiel géocentrique (lié à la Terre) ou un référentiel héliocentrique (lié au Soleil) ? Expliquez pourquoi.
- Le référentiel lié au train est plus approprié pour décrire le mouvement du passager. En effet, dans ce référentiel, on peut simplement considérer la vitesse du passager par rapport au train. Utiliser un référentiel lié à la gare compliquerait l'analyse en combinant la vitesse du train avec celle du passager.
- Pour un satellite en orbite autour de la Terre, le référentiel géocentrique est généralement plus adapté. Ce référentiel permet de décrire le mouvement du satellite par rapport à la Terre, ce qui est utile pour des applications comme la communication ou la surveillance terrestre. Un référentiel héliocentrique serait moins pertinent pour la plupart des observations et utilisations courantes d'un satellite en orbite terrestre.
Exercice 3 : Modélisation d'un solide en rotation et translation
Considérez une roue de vélo qui roule sans glisser sur une surface plane. Cette roue effectue à la fois un mouvement de translation (déplacement en ligne droite) et de rotation (tourne autour de son axe).
Analysez la trajectoire de deux points différents de la roue pour comprendre comment le choix du point affecte la description du mouvement.
- Décrivez la trajectoire que vous attendez pour le point situé au centre de la roue de vélo.
- Analysez la trajectoire d'un point situé à l'extrémité de la roue, vous pouvez tenter de la dessiner (par exemple, un point sur le bord extérieur de la roue).
- Le point situé au centre de la roue de vélo se déplace en ligne droite, ce qui représente le mouvement de translation rectiligne de la roue.
- La trajectoire d'un point situé à l'extrémité de la roue est une cycloïde, comme illustré ci-dessous :
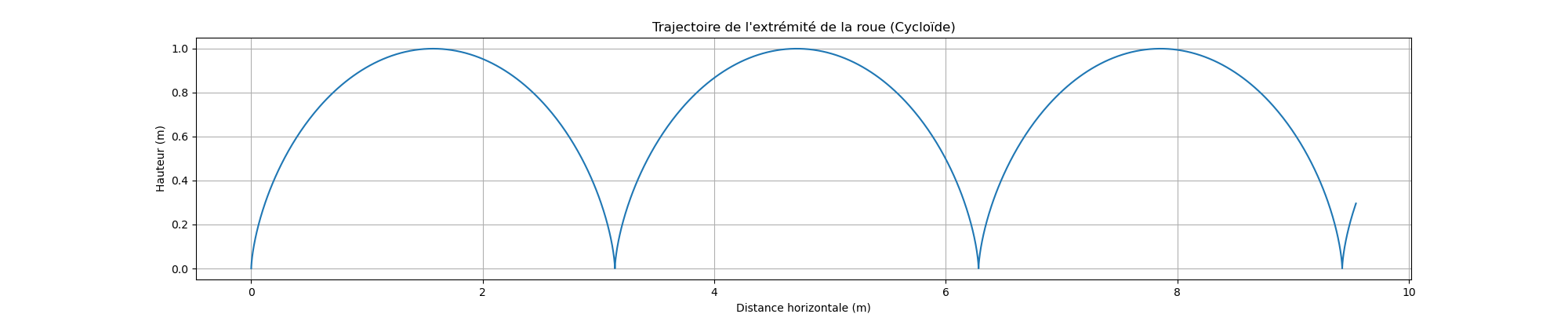
Exercice 4 : Comprendre les vecteurs de déplacement, vitesse moyenne et vitesse instantanée
Objectif : Cet exercice a pour but de clarifier la différence entre le vecteur déplacement, le vecteur vitesse moyenne et le vecteur vitesse instantanée d'un point en mouvement.
Prérequis : Assurez-vous de comprendre la notion de vecteur, qui est une quantité caractérisée par une magnitude (ou norme), une direction, un sens et un point d'application.
Imaginez un coureur qui parcourt une distance de 100 mètres en ligne droite de A (point de départ) à B (point d'arrivée). Il réalise cette distance en 10 secondes. À mi-chemin, sa vitesse instantanée est enregistrée à 12 m/s par un radar.
- Dessinez le vecteur déplacement du coureur de A vers B.
- Calculez la vitesse moyenne du coureur et dessinez le vecteur vitesse moyenne sur le même schéma.
- Représentez le vecteur vitesse instantanée à mi-chemin en utilisant les informations fournies par le radar.
- Le mouvement du coureur est-il uniforme ? justifier votre réponse.
La correction suivante contient les illustrations qui représentent les différents vecteurs étudiés.
Partie 1 : Vecteur Déplacement de A vers B
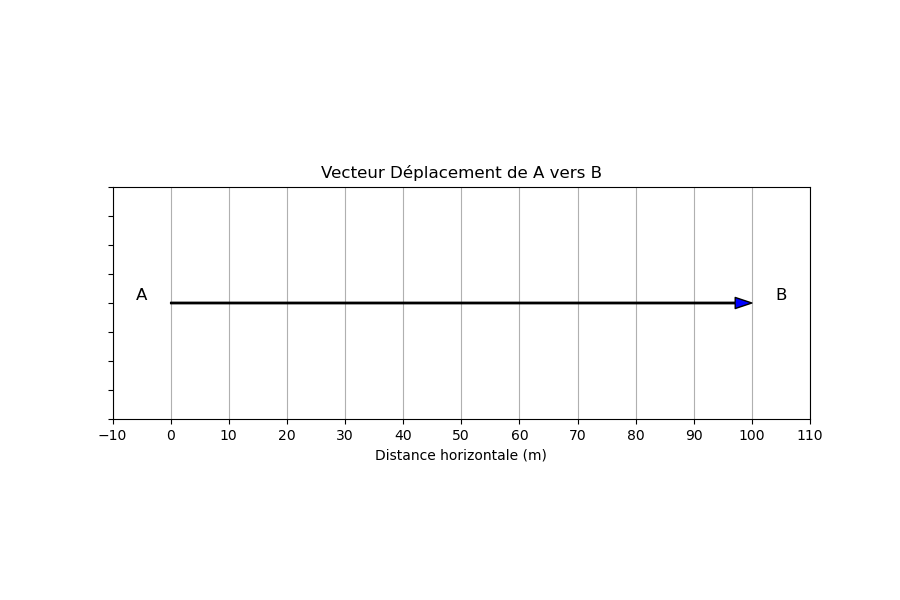
Partie 2 : Vecteur Vitesse Moyenne de A vers B
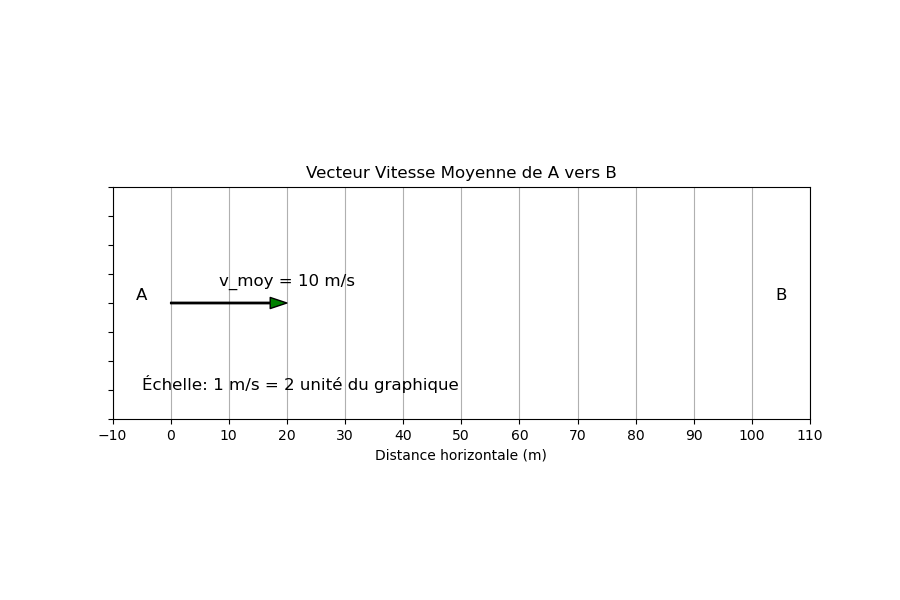
Partie 3 : Vecteur Vitesse Instantanée de A vers B
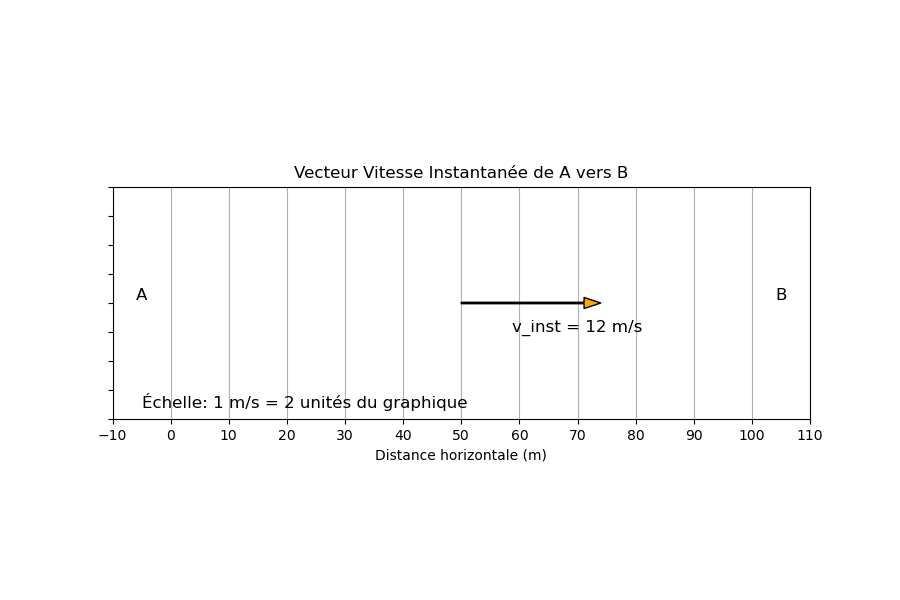
Le mouvement du coureur n'est pas uniforme car sa vitesse moyenne est différente de sa vitesse instantanée a mi chemin. Il y a surement une phase d'accélération au début et une phase de décélération à la fin. En tout cas la vitesse n'est pas constante sur l'entièreté du parcours
Exercice 5 : Analyse du Tir à Trois Points en Basketball
Objectif : Analyser en détail un tir à trois points au basketball, en mettant l'accent sur le choix du référentiel, la trajectoire, le point du système à étudier, et la représentation des vecteurs vitesse.
Prérequis : Compréhension des notions de trajectoire, de vecteurs, de référentiel en physique, et des connaissances de base en programmation Python (pour la partie avancée).
Partie 1 : Définition du Référentiel et Choix du Point du Système
Choisissez un référentiel approprié pour l'analyse du tir et discutez de la pertinence de ce choix. Déterminez également quel point du ballon (centre, surface, etc.) serait le plus judicieux à étudier pour comprendre le mouvement.
Partie 2 : Tracé de la Trajectoire et des Vecteurs Vitesse
Utilisez les coordonnées suivantes pour tracer manuellement la trajectoire du ballon et représentez les vecteurs vitesse pour chaque point. Précisez l'échelle choisie (par exemple, "1 cm représente 1 m/s").
| t (s) | x (m) | y (m) |
|---|---|---|
| 0 | 0 | 2 |
| 0.5 | 1 | 2.8 |
| 1.0 | 2 | 3.3 |
| 1.5 | 3 | 3.5 |
| 2.0 | 4 | 3.4 |
| 2.5 | 5 | 3.2 |
| 3.0 | 6 | 2.9 |
Partie 3 : Analyse et Réflexion
Analysez comment les vecteurs vitesse aident à comprendre le mouvement du ballon. Discutez de la manière dont ces vecteurs complètent l'information fournie par la trajectoire seule.
Partie 4 : Extension pour les Élèves Avancés (Utilisation de Python)
En tant que défi supplémentaire, les élèves qui le souhaitent peuvent refaire l'exercice en utilisant Python pour tracer la trajectoire et calculer les vecteurs vitesse. Cette partie est recommandée pour les élèves à l'aise avec la programmation.
Le référentiel choisi est le référentiel terrestre, avec le panier comme point de référence. Le point le plus judicieux du ballon à étudier est son centre, car cela simplifie l'analyse en évitant de tenir compte de la rotation du ballon.
-
L'image ci-dessous montre la trajectoire et les vecteurs vitesse du tir à trois points. Les vecteurs rouges représentent la vitesse et la direction du ballon à différents instants, illustrant clairement la dynamique du mouvement.
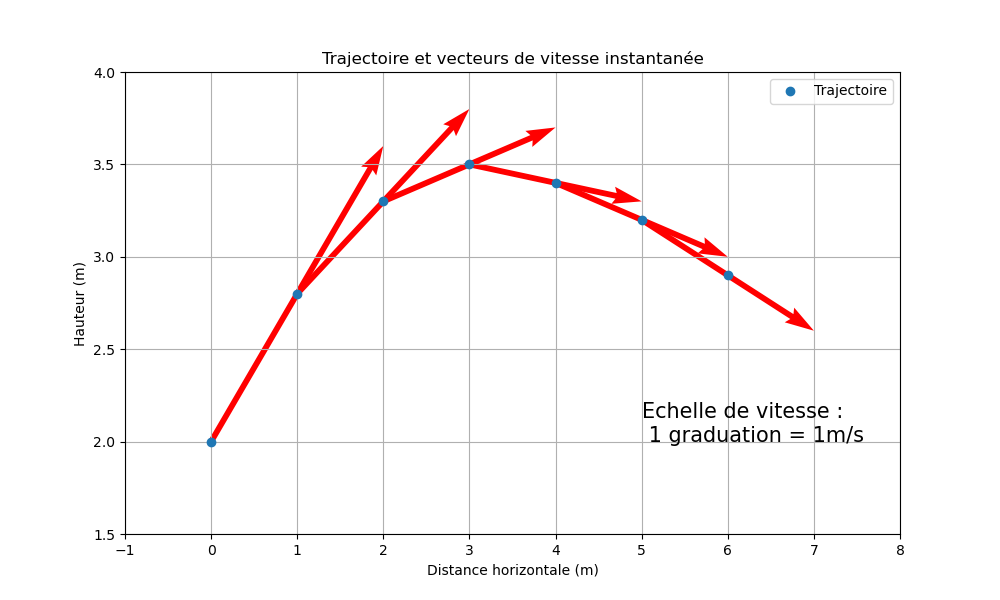
- Les vecteurs vitesse montrent que le ballon atteint sa vitesse maximale en milieu de trajectoire et ralentit à l'approche du panier. Ces vecteurs apportent une dimension supplémentaire à la simple trajectoire, en offrant des informations sur la vitesse et la direction du mouvement à chaque instant.
- A vous de jouer ;)